How To Use NPER Function In Excel
The NPER function is similar to both the Future Value and Present Value functions. But the difference is that the NPER formula will be returning the quantity of an investment, using the periodic, consistent payment and interest rate. NPER function calculates number of periods for an investment or a loan with the assumption of constant payments at regular intervals and a fixed interest rate.
Syntax is:
=NPER(rate,PMT,PV,FV,[Type])
- Rate – the rate of interest for the period
- PMT – fixed payment payed in each period,
- PV – present value of the investment or loan,
- FV – future value of an investment or loan (the value you want to achieve at the end of all periods)
- Type – specifies the time to make a payment during the period: 0 – payments are made at the ends of periods, 1 – payments are made at the beginning of each period.
The rate parameter should be provided for the payment period, ie if the interest rate is given annually and monthly payments are then divide the interest rate for 12 months.
For investment parameters PMT, PV and FV are negative positive, while for the credit PMT – negative PV – positive, FV – negative (if calculations are made assuming a partial repayment of a loan.
Basic calculation of NPER
How many payments you must pay to reach a value of 1 000 000 $ for investment with an annual interest rate of 10%? You pay monthly payments in the amount of 1 000 $, having already set aside 150 000 $. You pay at the end of each period (month).
Formula is =NPER(0.10/12,-1000,-150000,1000000,0)
Answer: Result is 171,43 what means, that you need 172 payments to reach 1 000 000$
Explanation:
- 0.10/12 – rate is 10% what must be divided by count of months
- -1000 – monthly payment (with minus because you have to pay)
- -150000 – your current cash (with minus because you pay)
- 1000000 – your future value (without minus because it’s your cash)
- 0 – because you pay at the end of the period
How much do you need to pay off your loan?
How many payments you need to pay off 100 000 $ loan repaid at the end of the month the installment of 700 $ (principal + interest). Annual interest rate is 8%.
Formula is
=NPER(0.08/12,-700,100000,0,0)
Answer: Result is 458,2 what means, that you need 459 payments to pay off this loan.
Explanation:
- 0.08/12 – rate is 8% what must be divided by count of months
- -700 – monthly payment (with minus because you have to pay)
- 150000 – your current cash (without minus because it’s your cash)
- 0 – your future value because you want to pay off this debt
- 0 – because you pay at the end of the period
NPER when you pay at the beginning of the month
How many months you have to pay to the bank at $300 to save the amount of $18 000. Annual interest rate is 3,5%. You pay at the beginning of each month.
Formula is
=NPER(0.035/12,-300,0,18000,1)
Answer: Result is 55,22 what means, that you need 56 months to reach $18 000.
Explanation:
- 0.035/12 – rate is 3.5% what must be divided by count of months
- -300 – monthly payment (with minus because you have to pay)
- 0 – your current cash
- 18 000 – your future value (without minus because it’s your cash)
- 1 – because you pay at the beginning of the period
Simple NPER Formula
The example is based on finding a solid NPER of the investment that we are about to make, so we can fully comprehend how the whole situation would work. This is something that would work with a full understanding of the formula, and we are getting the answer that we strive after with the formula.

Complete NPER Formula
The investment is going quite good, and we needs to know about the future value. This is a follow up to the previous example, and requires having a full formula in comparison to the previous example, and we are going to use the same data as previous one, so you could see the differences between the results. The example is about knowing the benefits of our investments, and how it would affect the ways that we are planning the executions of additional plans.

NPER Formula with Bigger than Symbol
The formula in this example includes using a mathematic symbol that will be beneficial in the long run. It is possible to make it possible to know how it will go when the rate is bigger than 10 percent. This example clarifies the possibilities of having a solid information about the number of investments when the rate is including such mathematical symbol. One great thing about this formula is that it provides the possibilities of knowing exactly how the mathematic symbol affects the outcome.

Usage of Formula with Future Value Increment
The formula is going to have a very specific formula that also include the increment of a future value. In this example, we would like to know how many times we needs to make an investment when we expect the future value to increase by 50%, and how it would affect the business deal and its overall performance.

A Formula with both NPER & AND
This example is a complete understanding of the formula, and we are going to use both NPER & AND for successfulness of acknowledging the information about how many times we will be making an investment when using two formulas simultaneously.

Additional Percentage with AND
In this example, we want to add some percentages to the current value, under circumstances that the business needs to add 12% to the current value, because we have accepted a customized deal with a company that is asking for 12 percent interest rate of the current value. This is where the NPER formula would be an excellent formula for acknowledging how many times the business needs to add the investment into its overall performance.

NPER with Texts
The example is about clarifying that under the circumstances that we have already labeled the cells with texts, to make it more understanding for us to understand which part of the formula the cell is talking about, even after some time has passed by, and we might have forgotten about what part of parameters belong to where in the NPER formula.
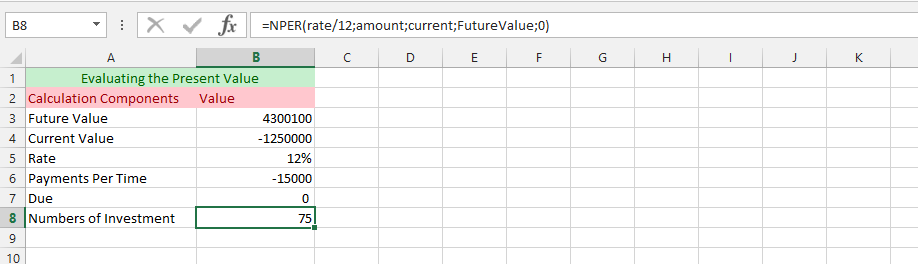
Simultaneously Using NPER with SUM
This example is using both the NPER and OR formulas simultaneously to find out how many times the company needs to perform the investments for it to successfully achieve a goal that has been set for the business. We have set a flexible rates for the business, and we would like to know how we would be making the investments.

Numeric NPER Formula
This is a more complicated formula, and we need to have a numeric formula of the NPER formula to get the answer that we are looking for with the formula. We want to make some evaluations, which is why we are rather having this kind of formula.
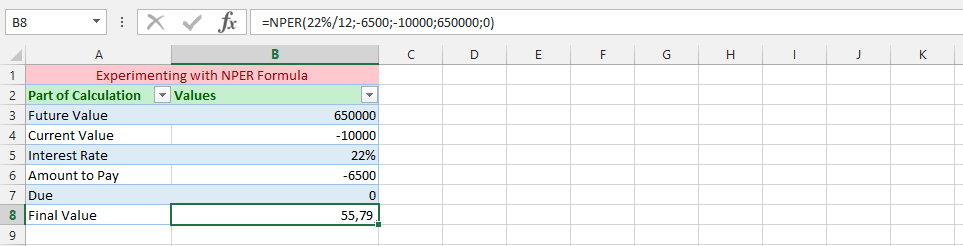
Understanding Usage of NPER Formula with another Spreadsheet
There are many different reasons that you’d might needs to have the NPER formula on another spreadsheet. But in this example, we are using a different spreadsheet, because we would like to have a full understanding of how many times we need to perform the investment for it to yield us the estimated future value, and we are using a different spreadsheet for it.

Template
Further reading: Basic concepts Getting started with Excel Cell References





